| Сотрудничество |
|
Поставьте себе на сайт и сообщите мне |
|
Статьи |
Теория информация (бомбы)
СКАЧАТЬ ШПОРУ ПО ТЕОРИИ ИНФОРМАЦИИ БОМБА!
Теорема: Если производительность источника сообщений H'(U)C, то можно закодировать сообщение таким образом, что ненадежность канала в единице времени будит меньше (H'(u)-с+E), где Е->0
Теорема. Несуществует способ кодирования, который обеспечит надежность в единице времени меньше, чем величина H'(u)-C
В такой форме теорема была дана Шенноном. В литературе формулируется следующим образом.
Если H'(u)>C, то способа кодирования, обеспечивающего высокую достоверность не существует.
Докозательство базируется на рассмотрении множества дискретных сообщений длинных последовательностей источника, их свойств.
Физический смысл т. Шеннона для канала с шумами:
Повышение вероятности при увеличении длительности кодирования сообщения заключается в том, что ч ростом времени увеличивается степень усреднения шума, дейтвующего в канале U. Следовательно степень его мешающего воздествия на кодирование.
Кодирование сообщения длинными последовательности может начатся, когда сообщение полностью поступило на кодер, а декодирование - на декодер.
Отсюда возникает задержка tзад=2Пи*t', где t' - время, которое уходит на кодирование, T-длительность последовательности кодирования символов.
Др. вывод? верность связи тем выше/меньше вероятность ошибки, чем длиннее блок кодированной последовательности (больше, чем (С-H'(U)))? которая определяет запас пропускной способности канала следовательно появляется возможность обмена вероятностью, задержкой и скоростью передачи.
На практике стараются уменьшить длину кодирования последовательности Т и пытаются добиться эффекта за счет применения помехоустойчивых кодов.
осн.часть кор.часть
|________|_________|
t' - время кодирования
Т - длительность последовательности кодирования символов.
1.Теор. - задача повышения скорости
2.Теор. - задача повышения достоверности
lcp=H/log(M)
Ис -> K1 -> K2 -> M -> Канал -> ДМ -> ДК2 -> ДК1 -> Получатель
Здесь решаются обе задачи. В локальной сети КК и ДКК не нужны. Для повышения надежности не нужны КИ и ДКИ.
Задачами теории кодирования явл:
1.Наилучшее согласование источника сообщения с каналом связи
ex: Достижение max скорости передачи информации
2.Обеспечение max правдоподобия/достоверности передачи сообщений
1-ая задача решается с помощью статистического кодирования
2-ая - с помощью помехоустойчивого кодирования
Начало теории кодирования заложил Клод Шеннон в 1946.
им сформулированно и достигнуто 2 основных результата:
1.Для канала без помех.
Кодирование можно осуществлять таким образом, что бы средняя длина сообщения не превышало некоторую величину lср>=h/log m
m - число букв в алфавите, когда закодировали.
Кодирование, которое учитывает это ограничение + статистические свойства источника называется статистическим.
Для канала с шумами существуют такие способы кодирования конечного кол-ва информации при котором достоверность передаваемой информации может быть сколь угодно высокой, если только скорость поступающей информации в канал не превышает пропускной способности канала.
Кодирование -> (Статистическое, Помехоустойчивое)
Кодированием называется отображение одной физической системы с помощью состояния физической системы.
ex: Кодирование звуков телефонии с помощью электрических колебаний.
два направления области кодирования оптимизируем
1)Кодер источника повышенной энтропии устраняет избыточность h=H/r
2)Ввод избыточности поввышает достоверность информации.
Пусть имеется система X (буквы русского алф) система может случайным образом принять одно из свих состояний.
m=32
Отобразим множество состояний X на множество состояний Y. Если m
ex: В азбуке Морзе буквы отоюражаются последовательной комбинацией символов ._ выбор комбинаций и установление соответствия между ними и букв системы x называется кодированием. Коды различаются по числу символов на которых формируется комбинация, др. словами числам сост. систему Y.
Одно и тоже сообщение мы можем закодировать различными способами. Возникает вопрос о наиболее выгодных оптимальных вариантах кодирования. Оптимальным считается такой код, который требует на передачу собщения минимум времени. Если может быть несколько кодов у которых время передачи одинаково, то оптимален, который имеет наименьшее кол-во элементарных символов.
ex: Знаки дорожного движения. Иконичный способ передачи информации.
Основные характеристики кодирования:
1.Длина кода (чем длиннее, тем хуже)
2.Основание кода (в 2-ой системе счисления {0,1}; На Украине 3-ная {-1,0,1};)
3.Мощность кода - кол-во кодов комбинации, которое можно создать для передачи сообщения.
4.Полное число кодовых комбинаций
ex: всего 16 (используется только 9 символов)
5.Число информационных символов. Кол-во разрядов, которое используется.
6.Число проверочных символов (для корректности кодов)
7.Избыточность кода.
R=1-log©/log(N)
c-мощность кода
N-полное число комбинаций
8.Скорость передачи кодовых комбинаций
9.Вес кодовых комбинаций. Кол-во единиц кодовых комбинаций
10.Кодовое расстояние. Число одноименных разрядов с различными символами.
11.Весовая характеристика кодов. Число кодовых комбинаций веса W, определенного веса.
12.Вероятность необнаружения ошибки. Вероятность того, что принимаемый код отличается от переданного, а св-ва данного кода не позволяют оределить факт наличия ошибки.
13.Оптимальность кода. Св-ва такого кода, который обеспечит мин вероятность необнаружения ошибки среди всех кодов такой же длины и такой же избыточности.
Билет №1
*****Основные проблемы ТИ
1-ая проблема:
1.Анализ сигналов как средства передачи сообщений, включающий вопросы оценки переносимого ими количества онформации
2.Анализ информационных хар-ик источниковсообщений и каналов связи, обеспечивающих точность кодирования и декодирования сообщений с предельной скоростью передачи как при наличие и отсутствии помех.
2-ая проблема:
Оптимизация системы связи в целом.
3-ая проблема:
связана с такой точкой зрения: К ТИ относят все те проблемы и задачи, в формулировку которых входит понятие информации. Ее предметом считают изучение процессов, сведенных к передаче, получению, хранению, и преобразованию информации.
ТИ - это математическая дисциплина, базирующаяся на вероятностых хар-ах.
проблымы информатики с точки зрения семантики(наука о знаках и словах).
Семантика->(классификация знаков) -> (иконическая(фото,рисунок), символьная(речь,слово), индексная)
Синтактика отражает структуру и строение объекта.
Семантика отображает связь между объектом и его обозначением.
Стигматика - выбор знака для отражения объекта.
Прагматика отображает потребительскую сторону и связана с практическим использованием объекта.
ТИ:(стрелочки)
1.Статистическая ТИ
2.Теория помехоустойчивого кодирования
3.Теория потенциальной помехоустойчивости
4.Семантическая ТИ
1.Мера информации
2.Создание помехоустойчивых кодов
3.Оценивает возможности передачи без помех и искажений.
4.Изучает смысл передаваемых сообщений
Важнейшие вклады отечественных и зарубежных ученых в создание и развитие теории информации:
1928г. - Р.Хартли предложил комбинаторную меру оценки кол-ва информации
1933г. - Котельников В.А. создал теорему о возможности представления непрерывной ф-ии совокупностью значений в отдельных точках отсчета
1941г. - Колмогоров внес огромный вклад в статистическую теорию колебаний, которая является мат. основой ТИ
1946г. - Котельников разработал оптимальные методы приема сигналов на фоне помех
1948г. - книга К. Шеннона "Мат. основа связи" - база современной ТИ.
==============================================
Билет №2
****Понятие информации
Информация есть отражение реального мира в нашем сознании с помощью органов чувств.
Под информацией понимаем не сами предметы и процессы, а их представительные хар-ки, которые образуют выделенные сущности.
Информация - это абстрактная категория.
Отражение - св-во индивидуального объекта воспринимать объекты реального мира.
(материя) -> [отражение] -> [первич.инфа] ->([чувственнный], [логический], [прагматический]) - способы получения
Чувственнный способ - с помощью 5 органов чувств. Отличается конкретностью. Можно измерить.
Логический - стат. усредненная хар-ка, связанная с обработкой класса однородных явлений или предметов.
Прагматический - связан с важностью, ценностью информации.
При отражении акцентируетсявнимание на восприятии объекта вцелом, в то время, как информация воспроизводит одну из сторон объекта à понятие отражения более содержательное и глубокое.
Материя -> Отражение -> Информация -> Гносиология
Делема ТИ:
1.Информация - это cв-во индивидуального объекта или процесса - это результат взаимодействия объектов или процессов.
2.Информация присуща не всем видам материи, присуща только определенным образом организованной материи (человек - организм, метеорит - не организм)
3.Информация содержится в любых процессах присуща только процессам управления.
Норберт Винер считает, что инф-я может возникнуть, а может исчезнуть.
Понятие информации связано с некоторыми моделями реальных вещей, отражающих их сущность в той степени, в какой это необходимо для практических целей.
======================================
Билет №3
****Объекты и явл. Система и процессы. Сигналы и сообщ. Дискр и непрер сообщ.
Информация -> (первичная (воспринимаем органами чувств)->вторичная (обработанная первичная инф-я))
Среды передачи определяют носитель информации.
Сигналы -> (Первичные "естественные" (-космические сигналы,-колебания воздуха), Вторичные "искуственные"(-создаются человеком,-радиосигнал))
Материальную основу сигнала составляют носители. Без носителей сигналы не существуют.
Информация не существует без носителей. Она не материальна, она проявляется в форме первичных сигналов или носителей.
[источник информации] -> сигнал -> [среда передачи] -> сигнал -> [получатель]
Информация, поступающая из космоса, непрерывная, аналоговая.
Информация -> (Непрерывная(непрер. ф-ия непрер. аргумента), Непрерывно дискретная, Дискретно непрерывная, Дискретная)
Носителями сигналов являются физические величины, такие как токи, напряжение, магнитные состояния.
Физические величины - ф-ии времени или имеют пространственное распостранение.
Определяющие:
-частота
-фаза
-амплитуда
-длительность импульса и т.д.
Эти пар-ры называют Информативными признаками. С их помощью передаются сообщения.
Сигнал считается Дискретным по данному параметру, если число значений четно.
Если же множество значений данного параметра образует бесконечную последовательность, то сигнал называется непрерывным по данному параметру.
Если же один параметр Дискретный, а второй - Непрерывный, то сигнал наз. Дискретно-непрерывным.
Аналоговый сигнал (от понятия "аналогичный") - аналогичный реальному сигналу.
======================================
Билет №4
****Источники информации
Источиник информации - это такой физический объект, система, явления, пораждающие сообщения.
Источники сообщений -> ( комбинаторные -> (конечные, бесконечные), Случайные "вероятностные" -> (Конечные, бесконечные))
В Комбинаторных источниках сообщения формируются путем комбинирования подмножеств множества сообщений, причем все сообщения равновероятны. Комбинирование происходит путем сочетания знаков исходного алфавита.
Случайные источники порождают сообщения, которые имеют разные вероятности.
Конечный Комбинации. Источник можно идентифицировать с подмножеством конечного множества.
Конечный Вер. Источник можно отождествить с распределением вероятности на конечном алфавите.
Бесконечный источник порождает бесконечные слова из букв алфавита или функции действительного переменного.
Вероятностные источники, обладающие конечной памятью, называются Марковскими.
Вероятностные источники без памяти - это такие, у которых вероятность появления очередной буквы не зависит от предыдущих букв. Такие источники называют Бернуллиевскими.
Эргодические источники создают случайные последовательности (эргодические). Такая последовательность удовлетворяет двум условиям:
-стационарность
-эргодичность
Стационарность означает, что вероятности отдельных знаков или букв в сообщении или их сочетании не зависят от расположения последних по всей длине сообщения.
Эргодичность означает, что статистические закономерности, полученные при исследовании 1 достаточно длинного сообщения с вероятностью, близкой к 1, справедливых для всех сообщений, которые создаются данным источником.
Стационарные источники сообщений, выбирающие каждый знак формируемой последовательности, независимо от др. знаков, называются Эргодическими.
==================================
Билет №5
****Информационные системы
Информационная система - автоматизированная система, определяющей особенностью которой является то, что она обеспечивает информацией пользователей из нескольких организаций. Именно этим она отличается, например, от управляющей системы реального времени, системы коммутации сообщений, среды программирования или персональной вычислительной системы. Рассматривая диапазон возможных значений слов "информация" и "система", можно предложить ряд более широких толкований термина "информационная система". Можно считать, например, что он относится ко всем автоматизированным системам или, в еще более широком смысле, ко многим системам, в состав которых не входят ЭВМ. Поэтому при рассмотрении только автоматизированных систем иногда употребляют
термин информационная система организационного типа.
Информационные системы предназначены для решения задач обработки данных, автоматизации конторских работ, а также задач, характерных для экспертных систем. Системы, основной функцией которых, является информационное обеспечение процесса управления, обычно называют управленческими информационными системами.
Информационный процесс=информация + {хранение, передача, преобразование} -инфа->[ИС]-инф.продукт->Информационные системы -> (информационно измерительные, системы передачи данных,
Системы искусств. интелекта, ИПС, ИСС, САПР, АСУ)
ИИС - системы, которые занимаются измерением
ИПС (информационно поисковая сичтема) - каталоги
ИСС (инф. справочная система)
АСУ(Автоматизированная Система Управления) - позволяет заменить человека при принятии решения.
САПР (Система Автоматизации Проэктирования Деятельности) - позволяет качественно моделировать
СИИ - ОС, система доставки человека на Луну. Один человек не может описать такую систему.Megabrain - СИИ.
Модель системы передачи данных:
[источник сообщений |ИИ][Пп(первич. преобр.)П-сообщ->[передатчик[Кодер][модулятор]]-сообщ->[канал связи]+[помехи]-сообщ с помех.->[приемник[ДеМодулятор][ДеКодер]]-сообщ->[получатель]
Источник информации - это такой физический объект, система, явление, пораждающие сообщение.
Сообщение - значение или изменение некоторой физической величины, которая отображает состояние объекта, системы, явления.
Как правило, первичные сообщения - это речь, музыка, изображение, изменение пар-ов окужающей среды, которые представляют собой ф-ию времени от любого аргумента не электрической природы. При передаче сообщения преобразуются в электрический сигнал, изменение параметров у которых и отображает сообщение.
Многие сообщения это команды исполнительным устройствам.
Телеграфные, текстовые сообщения дискретны. Сообщения, которые нельзя разбить на кванты, непрерывны. Значительная часть передаваемых сообщений не являются сигналами, а передаются пакетами.
================================
6. Кодирование информации как отображение состояний источника во внешней среде. Сжатие данных. Языки передачи сообщений. Модуляция сигналов.
Отображение множества состояний источника в множество состояний носителя называется способом кодирования, а образ состояния при выбранном способе кодирования - кодом этого состояния.
Кодирование – преобразование И к виду, удобному для передачи по каналу связи или хранению на материальных носителях. Требования к системам кодирования: экономичность, помехоустойчивость, однозначность.
Коды классифицируют на цифровые и символьные, равномерные и неравномерные, избыточные и неизбыточные, систематические и несистематические, а также корректирующие.
Любые методы сжатия данных основаны на поиске избыточной И и последующем ее кодировании с целью получения минимального объема. По существу, сжатие данных - это кодирование источника, которое приводит к уменьшению числа символов в сообщении до минимума, необходимого для представления всей информации сообщения или, по крайней мере, для обеспечения условий такого сообщения.
Существуют два класса методов сжатия И: 1) класс методов необратимого сжатия, имеющих также название энтропийного сжатия, или сжатия с потерями, 2) класс методов обратимого - восстановимого преобразования исходной И.
Хорошие результаты по сжатию можно получить только для определенного источника на основе точного знания его свойств.
Модуляция - процесс изменения одного сигнала, называемого несущим, в соответствии с формой некоторого другого сигнала. Несущий - это обычно аналоговый сигнал, выбираемый так, чтобы он наилучшим образом согласовывался с характеристиками конкретной системы передачи. Сигналы и способы модуляции могут сочетаться друг с другом с целью получения комбинированных сигналов, переносимых по нескольким независимым информационным каналам. К основным типам модуляции относятся: а) амплитудная модуляция (АМ), при которой сигнал несущей изменяется по мощности или амплитуде. Эта форма модуляции в системах передачи данных в чистом виде используется сравнительно редко; б) частотная модуляция (ЧМ), при которой изменяется частота несущей. Такой способ часто применяется в модемах; в)фазовая модуляция (ФМ), при которой изменяется фаза волны несущей. Этот способ модуляции часто используется в сочетании с амплитудной модуляцией в высокоскоростных модемах; г) импульсно-кодовая модуляция, при которой аналоговый сигнал кодируется сериями импульсов в дискретном потоке данных. Такая техника модуляции используется в устройствах кодирования-декодирования; д)спектральная модуляция (СМ), при которой волна несущей модулируется по частоте аналоговым или цифровым сигналом в сочетании с третьим, кодовым, сигналом. Такой способ применяется в военной технике в радиосетях с пакетной коммутацией
======================================
7. Модели сигналов. Дискретизация сигналов. Преимущества цифровой формы представления сигналов. Основная теорема Шеннона о кодировании для канала с помехами.
Сигнал – носитель информации, пересекающий пространство окружающей среды.
Модели сигнала: непр. ф-ия непр. аргумента, непр. ф-ия дискр. аргумента, дискр. ф-ия непр. аргумента и дискр. ф-ия дискр. аргумента(4 графика).
Дискретизация (квантование) - процесс формирования дискретного представления количественной характеристики, которая обычно имеет непрерывный вид. Различают квантование по уровню и времени. Уровень квантования - одно из значений непрерывного сигнала, полученное в результате его квантования, шаг квантования - разность между соседними уровнями квантования. Квантованием во времени называется измерение в дискретные промежутки времени амплитуды непрерывного сигнала. В результате замены мгновенного значения сигнала U соответствующим уровнем квантования V возникает погрешность р = U - V, которую называют ошибкой квантования. Эта погрешность является случайной величиной. При квантовании сигнала U(t) по уровню случайный процесс заменяется ступенчатой зависимостью - U1(t). Изменяющуюся во времени ошибку квантования d(t), также представляющую собой случайный процесс, называют шумом квантования d(t) = U(t) - U1(t).
Для представления цифровых данных при их передаче используются дискретные сигналы, принимающие конечное множество значений. В системах с гальванической связью для представления дискретных величин (обычно 0 и 1) используются различающиеся значения напряжения (или тока).Цифровой передаче данных свойственны весьма низкие значения коэффициента ошибок и довольно высокие скорости. Слабые сигналы можно регенерировать, сохраняя при этом суммарную вероятность ошибки на довольно низком уровне. Поскольку при цифровой передаче используются только логические нули и единицы, сигналы от нескольких источников легко уплотнять цифровыми методами.
Преимущества цифровых методов:
- упрощение работы с памятью (например, последовательности отсчетов можно воспроизводить при разных скоростях и в разных направлениях)
- расширение набора используемых арифметических операций
- повышение допустимой сложности алгоритмов
- возможность беспредельного увеличения точности вычислений.
Главный недостаток цифровых методов заключается в том, что для некоторых специфических приложений они оказываются более медленными, чем аналоговые методы.
Теорема Шеннона: для канала связи с шумами существует такой способ кодирования конечного количества информации, при котором информация будет передана с какой угодно высокой достоверностью, если только скорость поступления ее не превышает пропускную способность канала связи.
Пусть Н – энтропия источника, С – пропускная способность канала связи. Если Н<=С то существует такая система кодирования, при которой сообщения могут бфть переданы со сколь угодно малым искажением.
Если Н>С, то наименьшее искажение ограничено величиной Н-С.
========================
8. Каналы передачи сообщений. Влияние шумов. Преодоление помех. Теорема В.А.Котельникова.
Канал передачи сообщения - путь передачи информации со всеми необходимыми схемами, который используется для пересылки данных между системами или частями системы. В случае интерфейса, состоящего из нескольких параллельных каналов, каждый канал выделяется для передачи информации одного типа, например, данных или сигналов управления.
В соответствии со структурой входных и выходных сигналов выделяют дискретные и непрерывные сигналы. В дискретных каналах сигналы на входе и выходе представляют собой последовательность символов одного или двух(по одному для входа и выхода) алфавитов. В непрерывных каналах входной и выходной сигналы представляют собой функции от непрерывного параметра времени. Бывают также смешанные или гибридные каналы, но тогда обычно рассматривают их дискретные и непрерывные компоненты отдельно.
Шум - любой сигнал с небольшой амплитудой, который возникает в электронной или коммуникационной системе, и не является передаваемым и полезным. Шумы могут появляться, например, от внешних неблагоприятных воздействий и расстраивать систему, поскольку они могут формировать ложные сигналы, т.е. ошибки.
Шум квантования - действующий непрерывный шум, наложение которого на непрерывный сигнал приводит к тому же результату, что и квантование непрерывного сигнала по амплитуде. Эффект квантования во времени тоже может быть описан как наложение шума.
Помеха - любой короткий по времени и большой по амплитуде сигнал, который возникает в электронной или коммуникационной системе и не является передаваемым полезным сигналом (случайное колебание, значение некоторых параметров которого предсказать невозможно).
Методы борьбы с помехами:
1) Аппаратные;
2) Параллельные каналы связи;
3) Многократная передача данных;
4) Обратные связи;
5) Помехоустойчивое кодирование.
В.А.Котельников, ученый, внесший огромный вклад в теорию информации (в 1946 г. им защищена докторская диссертация "Теория потенциальной помехоустойчивости при флюктационных помехах"), построил математическую модель "идеального приемника", лучше которого по помехоустойчивости принципиально никакой приемник быть не может. Затем исследовал воздействие на этот приемник флюктационных шумов, наиболее сильно искажающих сигнал и наиболее часто действующих в системах связи.
Из полученных формул следовало, что полностью исключить действие помех можно только в двух практически не реализуемых случаях: при бесконечной мощности сигнала или при мощности помех, стремящейся к нулю.
Во всех остальных случаях полностью избавиться от действия помех невозможно. В частности, при передаче сигналов ДА-НЕТ (0 или 1) вероятность ошибки, то есть отношение искаженных посылок к их общему числу, определяется только отношением энергии сигнала к энергии помех при данном способе их передачи.
В.А.Котельников изучал передачу сигналов без избыточности, то есть никаких дополнительных элементов, кроме необходимых для переноса информации , в сигнале не было.
Результат В.А.Котельникова относится к системам безызбыточного кодирования.
===================================
9. Приемник информации. Демодулирование и декодирование информации. Достоверность получения информации.
Примемник информации: состоит из демодулятора и декодера.
Демодулятор – устройство, преобразующее входные аналоговые сигналы в выходные цифровые, выделяет полезный сигнал на фоне помех.
Принцип работы обратен принципу работы модулятора.
Модуляция - процесс изменения одного сигнала, называемого несущим, в соответствии с формой некоторого другого сигнала. Несущий - это обычно аналоговый сигнал, выбираемый так, чтобы он наилучшим образом согласовывался с характеристиками конкретной системы передачи. Сигналы и способы модуляции могут сочетаться друг с другом с целью получения комбинированных сигналов, переносимых по нескольким независимым информационным каналам. К основным типам модуляции относятся: а) амплитудная модуляция (АМ), при которой сигнал несущей изменяется по мощности или амплитуде. Эта форма модуляции в системах передачи данных в чистом виде используется сравнительно редко; б) частотная модуляция (ЧМ), при которой изменяется частота несущей. Такой способ часто применяется в модемах; в)фазовая модуляция (ФМ), при которой изменяется фаза волны несущей. Этот способ модуляции часто используется в сочетании с амплитудной модуляцией в высокоскоростных модемах; г) импульсно-кодовая модуляция, при которой аналоговый сигнал кодируется сериями импульсов в дискретном потоке данных. Такая техника модуляции используется в устройствах кодирования-декодирования; д)спектральная модуляция (СМ), при которой волна несущей модулируется по частоте аналоговым или цифровым сигналом в сочетании с третьим, кодовым, сигналом. Такой способ применяется в военной технике в радиосетях с пакетной коммутацией.
Декодер – декодирует на базе сигнала сообщения и представляет его в исходном виде.
Принцип работы обратен принципу работы кодера.
Кодирование – преобразование И к виду, удобному для передачи по каналу связи или хранению на материальных носителях. Требования к системам кодирования: экономичность, помехоустойчивость, однозначность.
Коды классифицируют на цифровые и символьные, равномерные и неравномерные, избыточные и неизбыточные, систематические и несистематические, а также корректирующие.
Мера соответствия принятого сообщения переданному определяет верность или достоверность передачи. То есть достоверность – самая главная цель системы передачи сообщений.
===========================================
10. Структурные меры информации: геометрическая, комбинаторная и мера Хартли. Примеры структурной оценки информации.
Меры информации: Структурные, статистические, семантические.
Структурная мера позволяет учитывать дискретное строение информационного комплекса.
Структурные меры информации: - геометрическая, комбинаторная, мера Хартли (аддитивная). – рассматривает дискретное строение источника информации.
Геометрическая мера – определяет потенциальное количество информации в заданном комплексе.
Информационный элемент – неделимая часть или квант информации в дискретных моделях, в реальных комплексах, а также элементы алфавита и числовых систем.
Информационная емкость – вычисляется как сумма по всем измерениям. Выражается числом, которое показывает, какое количество информации содержится в полном массиве информации.
Q=(x - величина, T – время, N - пространство)
Макс. значения по осям – X, T, N.
Интервал квантования или измерения – dX, dT, dN.
Мощности источника – MX = X/dX; MT = T/dT; MN = N/dN.
Полная мощность комлекса – M = MX*MT*MN.
I = logM=logMX+logMT+logMN = IX+IT+IN.
Комбинаторная мера выражается в количестве элементов, в количественных связях между ними, комбинациями из них.
К комбинаторной мере прибегают тогда, когда требуется оценить возможность передачи информации различными способами.
Комбинаторика – одна из форм кодирования информации.
Количество информации, которое измеряется с помощью комбинаторной меры, вычисляется количеством различных комбинаций.
Комбинирование возможно только при наличии нескольких элементов и переменной связи, а также множества разнообразных позиций.
Элементы неодинаковые – отличаются друг от друга любым признаком.
Одинаковые элементы могут стать неодинаковыми, если учесть их позицию или местоположение.
Комбинации – сочетания, размещения, перестановки с повторениями и без.
В комбинаторной мере возможное кол-во информации совпадает с числом возможных соединений, следовательно, определение кол-ва информации в К,М заключается не в простом подсчете квантов, а в определеннии кол-ва взаимных или действительно осуществимых комбинаций, т.е. в оценке структурно разнообразного информационного комплекса. В этом случае кол-во информации, по сравнению с геометрической многократно увеличывается.
Для аддитивной меры Хартли имеет важность длина и глубина числа. Глубина числа определяется количеством элементов или знаков, которое содержится в исходном алфавите. Соответствует основанию СС.
Q=h^l, h – глубина, l – длина числа.
Q’=log(h^l)=l*log(h) – 1928 год.
Мера Хартли, выраженная в битах, соответствует элементарному событию, которое может произойти или не произойти.
Аддитивная мера удобна тем, что обеспечивает аддитивность сложения и пропорциональность количества информации глубине числа l.
I = h^l -> I = l*log(h)
h = 2 -> I’ = l*log2 = l.
I = l бит.
I’=log2(n) – Клод Шеннон, все состояния равновероятны.
==================================
11. Статистические меры информации. Вероятность и информация. Понятие энтропии. Соотношение энтропии и количества информации.
При статистическом подходе И рассматривается как сообщение о некот. исходе нескольких событий, кот. носят случайный х-ер или реализуются случайной величиной или ф-ией. При этом кол-во И ставится в зависимость от априорных вероятностей этих событий, величин, ф-ий.
Когда появляется сообщ. о часто встречающемся событии, вероятность кот. стремится к 1, т.е. к показателю полной достоверности, такое событие мало информативно равно как и противоположное событие, вероятность кот. стремится к 0, т.е. оно невозможно.
Большинство видов И можно свести к паре «событие - антисобытие». Именно эта пара явл. простым и неделимым квантом И. (p – успех, q – неуспех, q=1-p).
Когда p=q=0,5, мы имеем наибольшую неопр-ть в событиях. События можно рассматривать как исходы некоторого опыта, причем они составляют ансамбль или полную группу событий.
В кач-ве опыта может быть измерение некот. случайной величины, принимающей некот. случайные значения. Тогда каждое определенное значение имеют смысл исхода или элемент события.
В простом случае события явл. несовместимыми. Они образуют полную группу событий, в кот. обязательно реализуется одно из событий.
В общем случае вер-ти исходов явл. const, но они могут изменяться во времени в зависимости от условий и обстоятельств, тогда они становятся переменными, а события, кот. они описывают – нестационарными.
Чтобы измерить кол-во И, человек ставит себя на место приемника. В этом случае конкретное кол-во И он рассматривает как рез-тат выбора среди мн-ва возможных вариантов сообщ, причем выбор осуществляется по заранее определенному правилу.
Понятие «выбор» несет в себе важный смысл: кол-во И связано с неопр-тью или неправдоподобием конкретной И безотносительно к ее структуре.
Шеннон взглянул на все виды И совершенно с новой позиции. И несет уменьшение неопр-ти в наших знаниях. Принимая решение «Да» или «Нет» мы уменьшаем неопр-ть в 2 раза. Если неопр-ть такова, что вероятности «Да» и «Нет» равны, то мы говорим, что наше решение несет И в 1 бит.
Шеннон доказал, что количественная оценка И, кот. несет 1 символ, требует неожиданности его появления, т.е. вероятности. Чем реже появляется символ или чем реже происходит некот. событие, тем меньше его вер-ть и тем больше несет кол-во И.
Неопр-ть каждой ситуации х-ся энтропией.
В физике:
В ТИ:
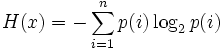
Таким образом, энтропия, полученная разными способами может отличаться коэффициентами перед знаком суммы.
Информация есть отрицание энтропии.
===========================================
12. Свойства энтропии. Энтропия как численная величина. Энтропия как статистический параметр. Виды энтропии.
Энтропия выражается как средняя И или средняя ф-ия мн-ва вер-тей каждого из возможных исходов опыта.
Энтропия м.б. определена также как среднее кол-во И на одно сообщение или мат. ожидание для измеримой величины.
Свойства энтропии:
1.Всегда неотрицательна.
2.Энтропия равна 0, когда вероятность одного из событий равна 0.
3.Энтропия максимальна в случае равновероятности. В этом случае аддитивная мера Хартли и логарифмическая мера Шеннона совпадают. Это совпадение свидетельствует о полном использовании информационной емкости системы. В случае неравных вероятностей количество информации по Шеннону меньше информационной емкости системы.
4.Энтропия является непрерывной функцией вероятности.
5.для источников с одинаковой вероятностью событий p=1/N энтропия увеличивается с ростом числа N.
6.Разложение процедуры выбора событий на несколько этапов не изменяет энтропию(процедуру выбора можно свести к последовательным двоичным решениям).
Принято считать, что кол-во И, содержащейся в дискретной И, надо измерять величиной исчезнувшей неопр-ти.
Энтропия безусловная H(x) - это энтропия источника или среднее значение кол-ва информации выдаваемое источником на один символ. H(y) - энтропия приемника или среднее кол-во информации, которое приходится на символ, получаемый приемником.
Взаимная энтропия H(xy)- взаимная энтропия системы передачи приемник в целом или среднее кол-во информации на пару символов (это переданный или принятый символ)
Условная энтропия H(y|x) - это условная энтропия y относительно x или меа информации в приемнике, когда известно, что передается x.
Условная энтропия H(x|y) - это усл. энтропия y относительно x или мера информации в источнике, когда известно, что принимается y.
Если в системе (1) нет помех и искажений, то условная энтропия=0
Кол-во взаимной информации будет равно либо энтропии источника либо энтропии приемника.
В случае отсутствия статистической связи между источниками x и y условная энтропия источника y относительно источника x равна безусловной энтропии источника y. Это означает, что сигнал yi принадлежит Y является новой по отношению к сигналу xi принадлежит X.
При наличии жесткой статистической связи между источниками x и y условная энтропия источника y относительно x равна 0.
==================================
13. Совместная энтропия статистически независимых источников. Условная энтропия статистически зависимых источников сообщений.
Независимые источники: Если 2 независимых источника с объемами алфавитов М и К рассматривать как 1 источник, кот. одновременно реализует пары состояний мi и кi, то полагают что энтропия объединения равна сумме энтропий отдельных источников.
Зависимые источники: Рассмотрим 2 ансамбля X и Y, связанных между собой вероятностной зависимостью.
Суммируем столбцы матрицы и получаем схему объединения:
При оценке не опред. выбора часто приходится учитывать стат. Связи, кот. в большинстве случаев имеют место как состояние 2 или нескольких источников, объединенных в рамках системы, так и между соседними, последоват-но выбираемыми источниками.
Определим 2 статистически связанных ансамбля X и Y.
Вероятности p(yi xi) – совместная реализация взаимозависимых состояний xi и yi, кот. можно выразить через условную p(xi | yi) в соответствии с тем, что принять за причину, а что за следствие.
p(x y) = p(x)p(y|x)=p(y)
В рассмотренном случае частной условной вероятности:
Матрица p(xy) является основной характеристикой объединенного источника X и Y, кот. характеризуется этими вероятностями.
Вероятности p(xi yi) указывают на вероятности возможных комбинаций состояния xi источника X и состояний yi источника Y.
Энтропия объединения:
==========================
14. Совместная энтропия статистически зависимых источников сообщений. Взаимная энтропия источников.
Зависимые источники: Рассмотрим 2 ансамбля X и Y, связанных между собой вероятностной зависимостью.
Суммируем столбцы матрицы и получаем схему объединения:
При оценке не опред. выбора часто приходится учитывать стат. Связи, кот. в большинстве случаев имеют место как состояние 2 или нескольких источников, объединенных в рамках системы, так и между соседними, последоват-но выбираемыми источниками.
Определим 2 статистически связанных ансамбля X и Y.
Вероятности p(yi xi) – совместная реализация взаимозависимых состояний xi и yi, кот. можно выразить через условную p(xi | yi) в соответствии с тем, что принять за причину, а что за следствие.
p(x y) = p(x)p(y|x)=p(y)
В рассмотренном случае частной условной вероятности:
Матрица p(xy) является основной характеристикой объединенного источника X и Y, кот. характеризуется этими вероятностями.
Вероятности p(xi yi) указывают на вероятности возможных комбинаций состояния xi источника X и состояний yi источника Y.
Энтропия объединения:
Взаимная энтропия: H(xy) = H(yx)
Характерное соотношение:
H(xy) = H(x) – H(x|y) = H(y) – H(y|x) = H(x,y) – H(x|y) – H(y|x).
Понятие взаимной энтропии соответствует взаимной информации.
Последовательность символов x1..xn, вырабатываемая источником X может претерпевать искажения на пути к приемнику, символ xi может стать yj.
Взаимная энтропия – энтропия системы “передатчик – приемник” в целом или среднее кол-во информации на пару символов – переданный и принятый.
Кол-во взаимной информации равно либо энтропии источника либо энтропии приемника.
I(x,y) = H(x,y) = H(x) = H(y).
На основании стат. данных могут быть установлены вероятности событий при условии, что имели место быть события.
=============================================
15. Алгоритмический подход к оценке количества информации. Количество информации и избыточность.
Выдвинутый А.Н.Колмогоровым тезис о том, что наряду с уже признанным вероятностным подходом к определению количества информации правомерны, а во многих ситуациях и более естественны, иные подходы: комбинаторный и алгебраический, привел к созданию нового раздела науки - алгоритмической теории информации.
При алгоритмическом подходе учитываются не только все вероятностные закономерности, но и другие (если они есть); если других закономерностей нет, то алгоритмический подход приводит к тем же результатам, что и вероятностный. Алгоритмический подход основан на применении теории алгоритмов для определения понятия энтропии, или сложности, конечного объекта и понятия информации в одном конечном объекте о другом. С помощью теории алгоритмов можно определить сложность описания различных объектов. Так, по А.Н.Колмогорову "относительной сложностью" объекта y при заданном x считается минимальная длина l(p) "программы" p получения y из x. Сформулированное так определение зависит от "метода программирования". Метод программирования есть не что иное, как функция ф(р,x) = y ставящая в соответствие программе p и объекту x объект y.
Избыточность - введение в систему дополнительных компонентов сверх минимально необходимого их числа с целью повышения надежности и работоспособности системы.
Следствием ограничений на выбор источником знаков является недоиспользование их как переносчиков инф-ии. Известная априорная? инф-ия о вероятностях выбора знаков и их сочетаний приводят к уменьшению ср-й неопределенности выбора источников знака, а следовательно, и переносимого им кол-во инф-ии.
Мерой избыточности является величина D, которая показывает, на сколько хорошо используются знаки данного источника.
D=(Hmax(x)-H(x))/Hmax(x)=(log(Lx)-H(x))/log(Lx)=1-H(x)/log(Lx)
Hmax(H) – считаем, когда Рi равновероятностные события.
Lx – кол-во букв в алфавите х.
D – Относительная избыточность.
В двоичном D2=1-H(x)/1=1-H(X)
Если избыточность источника равна 0, то формирование им сообщений оптимально в смысле наибольшего количества переносимой инф-ии, и мы можем подсчитать кол-во знаков, если нам известно кол-во инф-ии.
К=I/Hmax(x) знаков, когда отсутствуют помехи.
Т.к. в реальных условиях энтропия сообщений формируется источником, который обладает избыточностью всегда меньше максимального (Hmax), то для передачи того же кол-ва инф-ии потребуется:
K2=I/H(x)>K1 знаков.
Поэтому говорят об избыточности знаков сообщения и хар-ся тем же D;
D=(K2-K1)/K2=(Hmax(x)-H(x))/Hmax(x);
Полное устранение избыточности позволит увеличить эффективность использования букв почти в 3 раза.
Избыточность также бывает:
1) Структурная – дублирование каналов связи с определением принятой информации по мажоритарному принципу.
2) Временная – многократная передача данных, достоверность которых определяется либо по мажоритарному, либо по статистическому принципу.
3) Функциональная – передача данных с использованием обратной связи.
========================
16. Семантические меры информации. Целесообразность информации. Динамическая энтропия. Другие меры полезности информации: энтропия, шум, тезаурус.
Проблемы семантического уровня связаны с формализацией смысла передаваемой инф-ии, например, введение количественных оценок близости инф-ии к истине, т.е. оценок ее кол-ва. Эти проблемы чрезвычайно сложны, т.к. смысловое содержание инф-ии больше зависит от получателя, чем от семантики сообщения, представленного в каком-либо языке.
На прагматическом уровне интересуют последствия от получения и использования данной инф-ии абонентом. Проблемы этого уровня – это проблемы эффективности. Осн. сложность здесь состоит в том, что ценность или потребительская стоимость инф-ии может быть совершенно различной для различных получателей. Кроме того, она существенно зависит от истинности и прогностичности инф-ии, своевременности ее доставления и использования.
Тезаурус – (от греч. – сокровище) словарь, в кот. Указаны только значения отдельных слов, но и смысловые связи м/д. ними. Семантическая оценка кол-ва И существенно зависит от тезауруса получателя.
Тезаурус получателя определяет его на уровне знаний. Если сообщение изменяет тезаурус получателя, оно содержит для него некоторое кол-во инф-ии. Прагмати-й подход к опред. кол-ва инф-ии часто используется при анализе процессов управления. Основой оценки является ценность информации I как изменения вероятности достижения цели при получении этой инф-ии:
I=logP1-logP0=logP1/P0;
Р0-начальная вер-ть достижения цели;
Р1-вероятность достижения цели после получения инф-ии.
Возможны 3 случая:
а) Р1=Р0, тогда I=log1=0.Пустая без полезная инф-ия.
б) Р1>Р0, тогда I>0. Полезная инф-ия .
в) Р1<Р0, тогда I<0. Дезинформация.
================<<<ВСЕ>>>===================
|
| |
| Категория: Учебные статьи | Добавил: DiP_admin (21 Января 2014)
| Автор: Дмитрий E
|
| Просмотров: 3639
|
Добавлять комментарии могут только зарегистрированные пользователи. [ Регистрация | Вход ] |
|
|
 20 Февраля 2026, Пятница
20 Февраля 2026, Пятница 15:07
15:07
 20 Февраля 2026, Пятница
20 Февраля 2026, Пятница 15:07
15:07